

电机是一种电磁装置,其核心主要由绕组线圈和铁心等电磁部件组成,既然有线圈和铁心,就必然绕不开电感的问题。经常有同学张口闭口电机的电感如何如何,殊不知电机中的电感那讲究大了去了,自感、互感、相电感、线电感、直轴电感、交轴电感、主电感、漏电感、瞬态电感(电抗)、超瞬态电感(电抗)…这些令人眼花缭乱的电感都是怎么定义的?其物理意义又是啥?各种电感之间的关系是什么?这些电感怎么测量、怎么使用?本期就详细说说电机中电感的那些事。
一、什么叫电感
说起“电感”,通常有两个含义:一是指一种带有线圈的电磁器件,也称电感器或电抗器;二是指线圈固有的一种电气参数,通常用“L”表示,其单位为:亨利(简称亨H)、毫亨(mH)、微亨(μH)等,我们这里所说的电感是指后者,线圈的电感又有自感和互感之分,单个线圈只有自感,多个线圈除了各自有自感外,如果它们的磁路之间存在相互联系,还会有互感之说。
1、单个线圈的自感
自感是描述单个线圈通以电流时产生磁场(磁通)能力的物理量。由物理知识可知,一个线圈通以电流时会在其周围产生磁场,通常用磁力线来描述其周围的磁场,如图1所示。
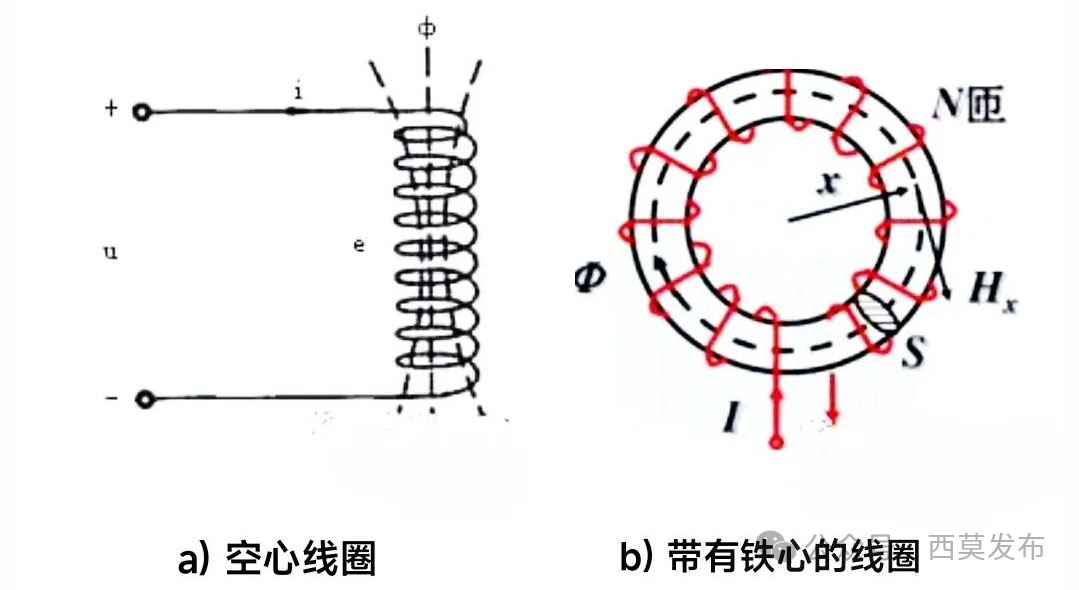
图1 线圈的自感
定义:线圈通以单位电流时产生的匝链线圈本身的磁链称为该线圈的自感,用L表示,即:
L=ψ/i ⑴
式中:L为线圈的自感(H);i为线圈中所通的电流(A),ψ为通电后线圈产生的匝链线圈本身的磁链(Wb),ψ=ΦN;Φ为磁通量;N为线圈匝数。通俗地讲就是给线圈通1A的电流能产生“几根磁力线”就叫线圈的自感是多少。式⑴被称为自感的定义式,常用该式来测定线圈的自感。
虽然线圈的自感如⑴式所示等于磁链除以电流,但自感的大小却与线圈是否通电流以及通电流大小无关(忽略磁饱和因素)。这就像一段导体的电阻R=U/I一样,虽然导体的电阻等于导体两端的电压除以导体中的电流,但一段导体的电阻大小却与是否通电以及通多大电流无关,导体的电阻只与导体的粗细、导体长度以及导体的材料有关,一段导体即使不通电,它的电阻该是多少还是多少,也就是说,导体的电阻是这段导体的一个固有参数,其大小只取决于这段导体的固有结构和材料。同理,线圈的自感也是线圈的固有参数,一个线圈绕制完成后,其自感就确定了,决定线圈自感大小的是线圈本身的固有结构。那么决定自感大小的因素有哪些呢?首先,线圈的自感与线圈的匝数有关,同样通1A的电流,绕两圈的线圈就比绕一圈的线圈产生的磁通量大,因此绕两圈的线圈就比绕一圈的自感大;其次,线圈的自感还与线圈磁路的磁导(磁阻)有关,也就是说,同样匝数和形状的线圈,如果是空心的,如图1a)所示,由于空气的磁导率很小,通1A电流产生的磁通就很少;如果把线圈绕在铁芯上,如图1b)所示,由于铁的磁导率远高于空气,同样通1A的电流产生的磁通就会多出许多倍,因此同样匝数和形状的线圈,带铁心的比不带铁心的自感要大许多倍。
当线圈的结构一定时,其自感为:
L=N²Λ ⑵
式⑵被称为线圈自感的决定式,它表明线圈的自感是由线圈本身的固有结构决定的,式中:N为线圈的匝数;Λ为磁路的磁导:
Λ=μ·S/l ⑶
式中:μ为磁路材料的磁导率,S为磁路的截面积,l为磁路长度。
2、初始电感、视在电感、增量电感
对于空心线圈,由于空气的磁导率为一常数,因此线圈的自感也是一个常数,人们常把空心线圈也叫做线性电感;对于有铁心的线圈,由于铁心存在磁饱和问题,铁心材料饱和后磁导率不再是个常数,因此线圈的自感也不再是一个常数,会和线圈所通电流大小有关,为此,需要把带有铁心的线圈自感进一步细分。如图2所示,为一带有铁心的线圈通电流时所产生的磁链与所通电流的关系曲线,其实就是铁心的磁化曲线。
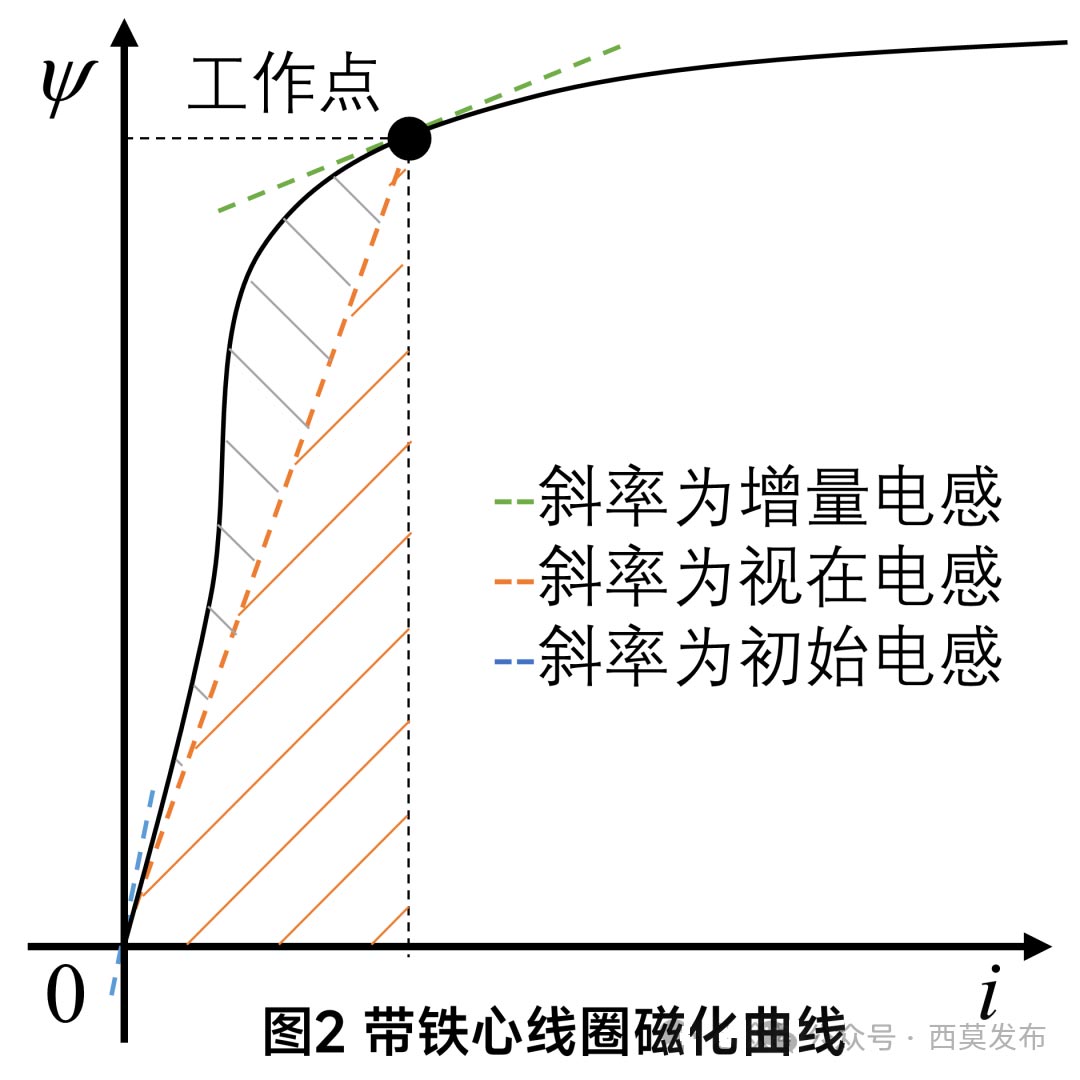
由图2和式⑴可知,当所通电流较小时,铁心不饱和,曲线近似为一直线,工作点的磁链与电流之比(ψ/i)近似为一常数,即自感可看作一个常数,我们将这一线性段的电感称为初始电感,也称为线圈电感的不饱和值,其大小为曲线初始段的斜率;随着电流的增大,铁心出现饱和现象,此时工作点的磁链与电流之比(ψ/i)不再是一个常数,意味着饱和后线圈的自感不再是一个常数,而是随着工作点的变化而变化,我们将此时的电感称为视在电感,由于饱和后工作点到原点的线段为磁化曲线的割线,视在电感(ψ/i)就是割线的斜率,因此视在电感也被称为割线电感。显然视在电感的大小与工作点的饱和程度有关,因此视在电感还被称为线圈自感的饱和值。除了上述两种电感外,还经常用到增量电感,所谓增量电感是指工作点处的增量磁链与增量电流之比(dψ/di) ,即磁化曲线上工作点处的切线斜率,因此增量电感也被称为切线电感。从各种电感的定义及图2可知,曲线初始阶段为直线,因此初始电感、视在电感、增量电感没有什么区别,在曲线膝点之前的线性区域可以近似认为视在电感与增量电感基本一致;随着饱和程度增加,增量电感和视在电感都会有所减小,当铁心达到深度饱和后,增量电感又趋近于一个常数。
电机绕组的视在电感常被用来分析电机的稳态特性,而增量电感常用来分析电机的动态性能,在电机控制中会经常用到。
3、线圈之间的互感
如果两个线圈共用一个磁路或两个线圈的磁路存在联系,其中一个线圈通以电流时,产生的磁通除了匝链本线圈外还匝链另一个线圈,那么这两个线圈除了各自存在自感外,它们之间还存在互感,如图3所示。
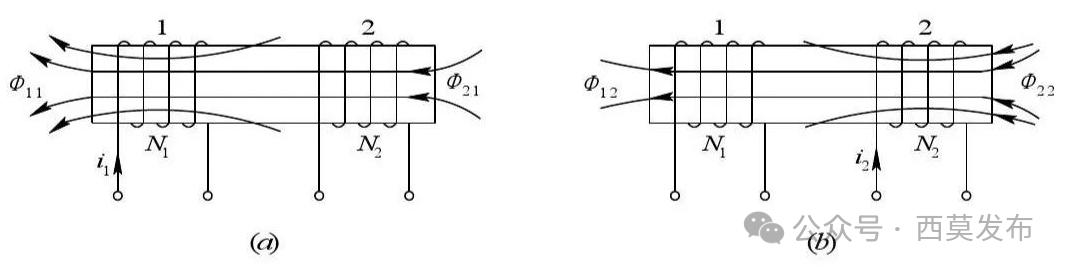
图3 两个线圈的互感
定义:在线圈1中通以单位电流产生的匝链于线圈2的磁链叫做线圈1对线圈2的互感,即L₂₁=ψ₂₁/i₁;同理,线圈2对线圈1的互感为L₁₂=ψ₁₂/i₂。理论和实践都表明:两线圈之间的互感大小取决于两个线圈两线圈的固有结构和相对位置,当两线圈的结构和相对位置一定时,它们之间的互感是可逆的,即:L₂₁=L₁₂。
4、线圈串并联时的等效电感
如果两个独立的线圈L₁和L₂,它们之间不存在互感,那么这两个电感线圈串联后的总电感就等于两个电感之和,即:L=L₁+L₂;这两个电感线圈并联后的总电感就等于两个电感之乘积除以两个电感之和,即:L=L₁L₂/(L₁+L₂),这一点和电阻的串并联规律是一样的。如果两个电感之间存在互感M,那么它们串并联后的总电感就远不像上面说的那么简单了,篇幅所限,我们这里只说结果,有关推导可自行参见物理或电工学相关文献。如图4所示为相互之间存在互感的两个线圈串联和并联的电路,其中:图4a)为两个存在互感的线圈正向串联(两个线圈的同名端顺串);图4b)为两个存在互感的线圈反向串联(两个线圈的同名端反串);图4c)为两个存在互感的线圈正向并联;图4d)为两个存在互感的线圈反向并联。
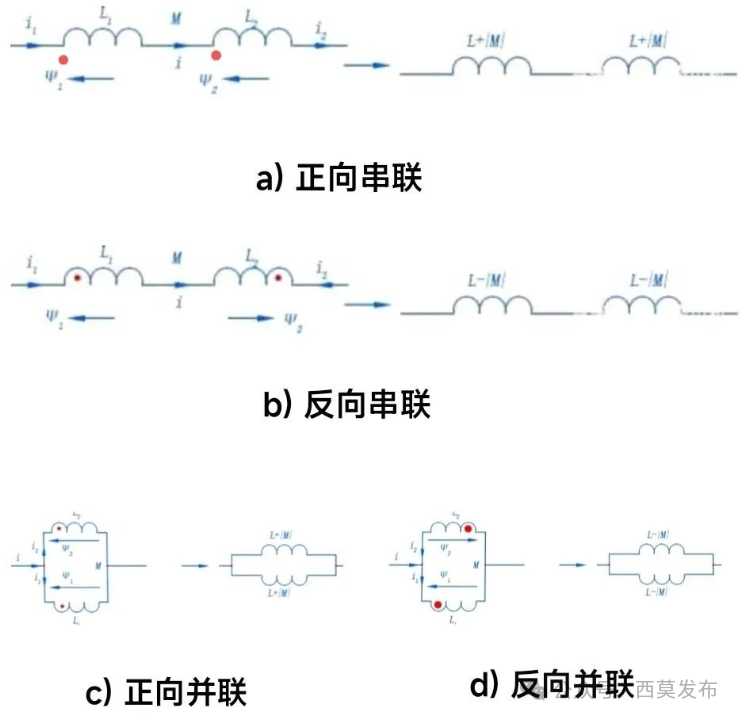
图4 两线圈存在互感时的串并联电路
对于图4a)和图4b)所示的串联电路,两个线圈串联后的等效电感为:
L=L₁+L₂±2M ⑷
式中的“±”号对于图4a)正向串联时取“+”;对于图4b)反向串联时取“-”。
对于图4c)和图4d)所示的并联电路,两个线圈并联后的等效电感为:
L=(L₁L₂-M²)/(L₁+L₂∓2M) ⑸
式中的“∓”号对于图4c)正向并联时取“-”;对于图4d)反向并联时取“+”。
复习完以上基本物理概念,接下来分析电机绕组的各种电感。
二、电机绕组的电感
1、转子对称时电枢绕组的电感
电机分交流电机和直流电机两种,这里仅分析交流电机的绕组电感。交流电机又分为同步电机和异步电机两种,无论是同步电机还是异步电机,其电枢绕组的结构都是一样的,电枢绕组通常为三相对称绕组,嵌装于定子侧,同步电机和异步电机的区别在于转子,异步电机的转子是一个圆柱形状的铁心内嵌装有三相对称绕组(绕线式)或笼型绕组(鼠笼式)。而同步电机的转子结构则种类繁多:有些嵌装有励磁绕组和阻尼绕组,称为电励磁同步电机;有些是装有永磁体用于励磁,称为永磁同步电机;还有些则是通过转子铁心的非对称形状形成非对称磁阻来产生电磁转矩,称为磁阻同步电机;除此之外还有些永磁电机,即可产生永磁转矩还可产生磁阻转矩,称为内嵌式永磁同步电机(IPM);还有些同步电机转子上即有励磁绕组又有永磁体,称为混合励磁同步电机。对于不同转子结构的交流电机,其定子绕组的电感特性是不同的,我们首先来分析对称转子的交流电机电枢绕组电感。
所谓对称转子,是指转子沿径向各个方向上磁阻相等,电机的主磁路磁阻与转子的位置无关,如:异步电机转子、隐极同步电机转子以及表贴式永磁同步电机的转子均可看作对称转子,如图5所示。
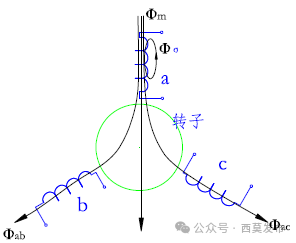
对于图5所示的对称转子电机,由于三相定子绕组的匝数相同,三相绕组轴线互差120°空间电角度,且各相绕组的磁路磁导与转子位置无关,因此,在忽略铁心饱和的情况下,各相绕组的自感均相等,且为常数;任意两相绕组之间的互感也相等,且为常数。
如果单独给某一相绕组(以A相为例)通入电流Iᴀ,产生匝链A相绕组自身的磁链为ψᴀᴀ;产生匝链B相绕组的磁链为ψʙᴀ;产生匝链C相绕组的磁链为ψᴄᴀ。将匝链A相绕组的磁链ψᴀᴀ分为漏磁链ψσ和穿越气隙的电枢反应磁链ψₐ两部分,即:ψᴀᴀ=ψσ+ψₐ。则由于B相绕组和C相绕组与A相绕组在空间上差120°电角度,故ψʙᴀ=ψᴄᴀ=-(1/2)ψₐ。根据电感的定义,各相绕组的自感及相互之间的互感分别为:
Lᴀᴀ=Lʙʙ=Lᴄᴄ=(ψσ+ψₐ)/Iᴀ=ψσ/Iᴀ+ψₐ/Iᴀ=Lσ+Lₐ
Lᴀʙ=Lʙᴄ=Lᴄᴀ=-(1/2)ψₐ/Iᴀ=-(1/2)Lₐ ⑹
式中:Lσ=ψσ/Iᴀ,为一相绕组的漏电感;Lₐ=ψₐ/Iᴀ,为一相绕组的电枢反应电感。
虽然根据⑹式可以得出三相绕组独立的自感和相互之间的互感,但在对称转子的电机中,这些独立的电感参数并不常见,特别是在电机的稳态分析时,这些独立的电感参数意义并不大,只是在动态建模分析时才会用到。在异步电机、隐极同步电机等对称转子电机进行稳态分析时,通常采用三相绕组联合作用的电感(抗)参数来进行分析计算,推导等效电路,因此对于对称转子的电机,三相绕组联合作用下的电感参数更为常见,也更有意义。
如果在三相绕组中通入三相对称交流电流,就会在气隙中产生应该圆形的旋转磁场,同时在每相绕组中还会产生一定的交变漏磁。设三相绕组所通三相对称交流电流的幅值为Im,所产生的旋转磁场的每极主磁通为Φm,每相漏磁链为ψσ。由于每极主磁通Φm是三相绕组联合产生的,考虑到三相绕组之间互感,因此Φm应该是一相绕组单独通电产生的磁通Φₐ的1.5倍,即Φm=1.5Φₐ。主磁通Φm在旋转过程中会依次匝链各相绕组,从而在各相绕组中产生交变的磁链,交变磁链的最大值为ψm=1.5ψₐ,根据电感的定义,各相绕组的电感为:
Lᴀ=Lʙ=Lᴄ=(ψm+ψσ)/Im=ψm/Im+ψσ/Im=ψσ/Im+1.5ψₐ/Im=Lσ+1.5Lₐ=Lσ+Lm ⑺
式中:Lσ=ψσ/Im为漏电感;Lm=ψm/Im=1.5Lₐ为电机的主电感。在异步电机中Lm通常被称为激磁电感,对应异步电机等效电路中的激磁电抗;在隐极同步电机中Lm通常被称为电枢反应电感,对应隐极同步电机等效电路中的电枢反应电抗,主电感Lm与漏电感Lσ之和称为同步电感,对应同步电抗。
再次强调,上述根据电感定义求取各电感时,ψm并不是只针对某一相绕组通电流产生的磁链,而是三相绕组通入三相电流联合作用产生的磁链,与之相除的电流也不是某一相绕组的电流,而是三相绕组同时所通的三相电流的最大值,这就意味着⑺式中的各相绕组的电感是考虑了三相绕组之间的互感影响而得到的综合电感,也称主电感。这种考虑了三相绕组联合作用的效果得到的参数在电机学中称之为“三相系统”下的参数,这是有别于单个或多个独立线圈自感和互感参数的重要差别,如无特别说明,三相电机的电感参数都是指“三相系统”下参数(后续同)。
2、转子非对称时电枢绕组的电感
当转子各向磁导不对称(dq轴磁导不相等)时,称为非对称转子,如凸极同步电机和内嵌式永磁电机转子、磁阻同步电机转子等,由于绕组磁路的磁导与转子位置有关,所以各相绕组的自感和互感就成为了转子位置的函数,我们以电励磁凸极同步电机为例介绍转子非对称时电枢绕组的电感,如图6所示。
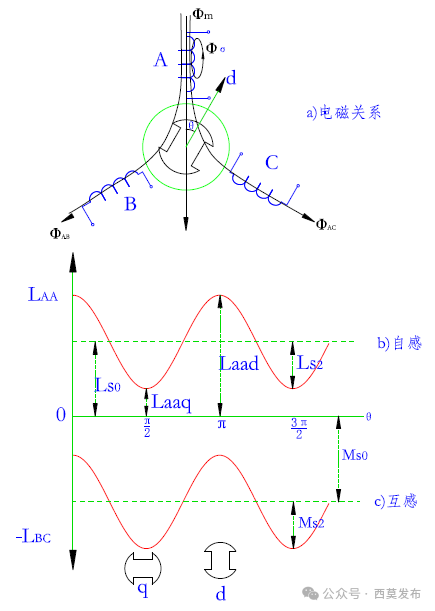
图6 转子非对称时电枢绕组的自感和互感
由图6可见,当转子直轴(d轴)对齐A相绕组轴线时,A相绕组的磁阻最小,如果此时给A相绕组单独通电流,产生的磁通最大,说明此时A相绕组自感最大;如果此时给B相绕组通电流,产生的匝链于C相绕组的磁通最小,说明此时BC相绕组之间的互感绝对值最小,设三相绕组的同名端都取绕组的首端,则三相绕组之间的互感实际值均为负值。同理,当转子交轴(q轴)对齐A相绕组轴线时,A相绕组自感最小,而BC相绕组之间的互感绝对值最大。随着转子位置的不同,自感和互感分别以一个恒定的平均值Ls₀和Ms₀为中心呈二倍频余弦规律波动,波动的幅度分别为Ls₂和Ms₂,如图6b)、图6c)所示,各相绕组的自感和互感为:
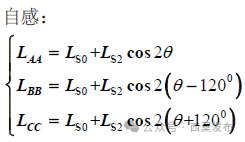
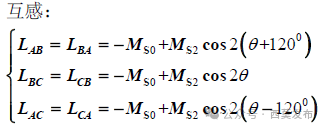
式中:
Ls₀=Lσ+(Laad+Laaq)/2
Ls₂=(Laad-Laaq)/2
Ms₀=Mσ+(Laad+Laaq)/4
Ms₂=(Laad-Laaq)/2
Lσ和Mσ分别为漏自感和漏互感;Laad和Laaq分别称为直轴和交轴对齐某相轴线时,该相绕组的电枢反应电感。
需要特别说明的是,上述⑻式和⑼式中的电感参数均为三相绕组各自独立的参数,并不是前面所说的“三相系统”下的参数。也就是说⑻式和⑼式中的自感和互感参数是指单独给某一相绕组通电时得到的自感和互感,并没有考虑三相绕组同时通电的联合作用效果。
3、直轴电感和交轴电感
以上讨论的是在定子abc坐标系下各相绕组的自感和它们之间的互感,其物理意义较为直观,各电感值就是实际绕组的电感值。
对于异步电机这样的各向均匀对称的转子,各相绕组的自感及互感均为常数,因此异步机可以得到一个以恒定绕组参数组成的等效电路。但对于同步电机而言,其绕组电感参数与转子位置有关,是转子位置角θ的函数,当转子旋转时θ就是时间的函数,因此绕组的自感和互感也就是时间的函数。虽然这些参数都是实际绕组的物理实际值,但由于参数随时间变化,用这些时变参数来分析电机的性能及各种方程式十分繁杂,为了简化同步电机的分析计算,需要转化为恒定的绕组参数,为此对于凸极同步电机,通常采用“双反应理论”进行分析。我们知道,三相对称绕组中通以三相对称交流电流时,会产生一个圆形的旋转磁势,而两个以同步转速旋转的正交的两相绕组中分别通以直流电流同样可以产生一个圆形的旋转磁势,这就为“双反应理论”奠定了基础。所谓“双反应理论”,就是把三相电枢绕组等效为两个正交的同步旋转绕组,其中一个绕组的轴线始终与d轴对齐,称之为d轴绕组;另一个绕组的轴线始终与q轴对齐,称之为q轴绕组。等效变换的原则是变换后dq绕组产生的旋转磁势等于原来三相绕组联合作用产生的旋转总磁势,只有这样才能保证变换前后电机内部的电磁关系和能量转换关系不变。通常有两种等效方法:一种是所谓的“等幅值变换”,即变换前后两种绕组中的电流、电压、磁链幅值相等,这种等效方法会导致用dq两相绕组计算出的功率与三相绕组计算出的功率不相等,在计算功率时需要乘以一个变换系数;另一种是所谓的“等功率变换”,即变换前后两种绕组的功率相等,当然这种变换前后的电流、电压、磁链幅值不相等。这两种等效变换方法分别适用于不同的场合,这里默认采用等幅值变换。这种等效变换其实就是一种坐标变换,首先把原来静止的abc坐标系下的三相电压、电流、磁链等物理量变换成静止的正交αβ坐标系下的两相绕组的物理量,使α轴线与a相轴线重合,β轴超前α轴90°,这一变换称为Clark变换(即3s→2s变换),当然也可以把静止的两相坐标变换回静止三相坐标,即Clark逆变换(2s→3s变换);然后再将静止的αβ坐标系下的各物理量变换为与转子上的dq旋转坐标系下的各物理量,d轴始终与转子N极中心线重合,q轴超前d轴90°,这一步变换就是通常所说的Park变换(即2s→2r),当然也存在Clark逆变换(2r→2s变换)。
等幅值Clark变换的变换公式(转换矩阵)为:

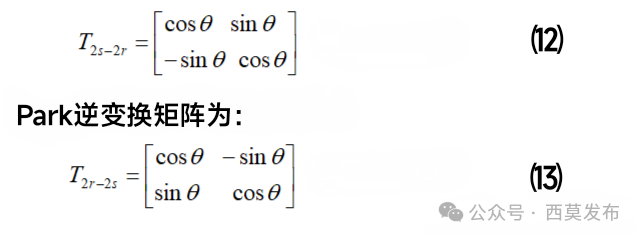
用上述转换矩阵可以实现电压、电流和磁链在不同坐标系下的转换,上述变换矩阵的推导过程可参见相关文献,篇幅所限在此不赘述。在原来静止的abc坐标系下,三相绕组的自感和互感都是转子位置的函数,如⑻式和⑼式所示,如果转子旋转,这些电感参数就是时变函数,非常复杂,难以计算分析,经过以上变换后,由于dq轴绕组随转子同步旋转,使得原来的三相绕组中的交流电压、电流和磁链变换成为dq绕组中的恒值电压、电流和磁链的直流量,电感也由原来随转子位置变化的量变成了恒定量,而且由于dq轴相互垂直,因此dq绕组间也不存在互感了。三相绕组电感变换为旋转dq轴绕组电感的公式为(推导过程略):
![]()
虽然按⒁式可以求出dq坐标系下的直轴电感Ld和交轴电感Lq,但求解过程的非常繁琐,而且不能体现交直轴电感的物理意义,纯属一种数学推导过程,为此我们还是从物理意义上对交直轴电感予以推导。根据绕组电感的定义,d轴绕组的电感Ld即为在d轴绕组中通1A的电流时所产生的磁链,即Ld=ψd/Id;q轴绕组的电感Lq即为在q轴绕组中通1A的电流时所产生的磁链,即Lq=ψq/Iq。由于Ld和Lq均是一个恒值,不再与转子位置有关,我们就不妨在转子d轴对齐A相轴线(θ=0°)时,给d轴通入Id=Im的电流,q轴内不通电流(Iq=0),此时d轴绕组产生的磁链为ψm,根据坐标变换等效原则,ψm应该与A相电流的瞬时值达到峰值(iᴀ=Im)、其余两相电流均为负的一半峰值(iʙ=iᴄ=-0.5Im)时三相绕组联合产生的磁链相等,即:
ψm=Ld*Id=Ld*Im=Lᴀᴀ(0°)*Im+Lᴀʙ(0°)*(-0.5Im)+Lᴀᴄ(0°)*(-0.5Im)=[Lσ+ Mσ +(3/2)Laad]Im ⒂
由⒂式得直轴电感:
Ld=Lσ+ Mσ +(3/2)Laad=Lσ +Mσ + Lad ⒃
同理,如果我们在q轴对齐A相相轴(θ=90°)时,给交轴绕组通电流,直轴不通电流(Id=0、Iq=Im),则q轴绕组产生的磁链ψm应该等于q轴对齐A相绕组轴线(θ=90°)时,A相电流达到峰值(iᴀ=Im)、其余两相电流均为负的一半峰值(iʙ=iᴄ=-0.5Im)时三相绕组联合产生的磁链,即:
ψm=Lq*Iq=Lq*Im=Lᴀᴀ(90°)*Im+Lᴀʙ(90°)*(-0.5Im)+Lᴀᴄ(90°)*(-0.5Im)=(Lσ+ Mσ +3Laaq/2)Im ⒄
由⒄式得交轴电感:
Lq=Lσ+ Mσ +(3/2)Laaq=Lσ +Mσ + Laq ⒅
式⒃和式⒅中:Lad和Laq分别为三相系统下的直轴电枢反应电感和交轴电枢反应电感,Lad=(3/2)Laad,Laq=(3/2)Laaq。由于d轴绕组和q轴绕组正交,因此二者之间不存在互感问题,即两绕组互感为0。
综上可见,经过以上变换,绕组的电感参数大为简化,由原来的三相时变量电感变为了dq轴上的恒定量,但其物理意义被弱化了,为了便于理解,有必要再进一步说明一下交直轴电感的物理意义:由以上推导可知,直轴电感Ld其实就是当转子d轴对齐某相绕组轴线时,该相绕组的自感;交轴电感Lq就是当转子q轴对齐某相绕组轴线时,该相绕组的自感。当然由于交直轴电感是三相系统下的参数,考虑到原来三相绕组之间存在互感,三相绕组同时通电时,除了要考虑本相绕组通电产生的磁链,还要考虑另外两相中的电流也会对该相绕组产生互感磁通,也就是把一相绕组的电枢反应电感Laad和Laaq放大3/2倍再加上其它两相绕组的漏互感,才能得到与三相系统完全等效交直轴电感。
4、相电感和线电感
经常有同学提到相电感、线电感。关于相电感,其实在前面的2.2节中已经讲得很清楚了,所谓“相电感”就是各相绕组自己独立的自感以及它们之间的互感,式⑻、式⑼和式⑹就是各相绕组的相电感,其中式⑻和式⑼对应非对称转子,由于非对称转子的磁导非对称,因此绕组的相电感与转子位置有关。如果是对称转子,则各相电感均为常数,与转子位置无关,由此可见,式⑹可以看作是式⑻和式⑼的一个特例,按式⑻和式⑼只计算恒定部分Ls₀和Ms₀即可,不存在交变部分Ls₂和Ms₂。
所谓“线电感”就是在三相绕组的任意两个出线端看进去的电感,因此“线电感”其实并不是某一相绕组的参数,而是多个绕组串并联后的等效电感参数。我们首先看三相绕组Y型接法时的线电感,如图7所示。
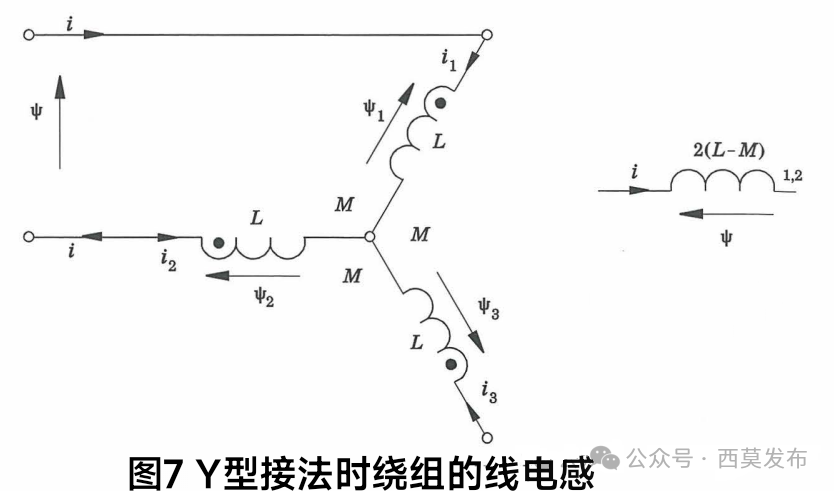
由图7可以看出,Y型接法的绕组线电感其实就是两相绕组反向串联时的等效电感,根据式⑷可得Y型接法的绕组线电感为:
Lʟʟ=2(L-M) ⒆
将⑻式和⑼式中相应的自感和互感代入⒆式,并整理得:
Lʟʟ=2(Lσ + Mσ)+(3/2)[(Laad+Laaq)-(Laad-Laaq)cos2θ] ⒇
由⒇式可见,在非对称转子电机中,线电感也是随转子位置角θ变化的,随着转子位置的不同,线电感总存在一个最大值Lmax和一个最小值Lmin。
对于内嵌式永磁电机,通常Laad<Laaq,因此线电感的最大值和最小值分别为:
Lmax=2[(Lσ + Mσ)+(3/2)Laaq]=2Lq
Lmin=2[(Lσ + Mσ)+(3/2)Laad]=2Ld(21)
对于电励磁同步电机,通常Laad>Laaq,因此线电感的最大值和最小值分别为:
Lmax=2[(Lσ + Mσ)+(3/2)Laad]=2Ld
Lmin=2[(Lσ + Mσ)+(3/2)Laaq]=2Lq (22)
对于三角形接法的绕组,线电感的等效电路如图8所示。
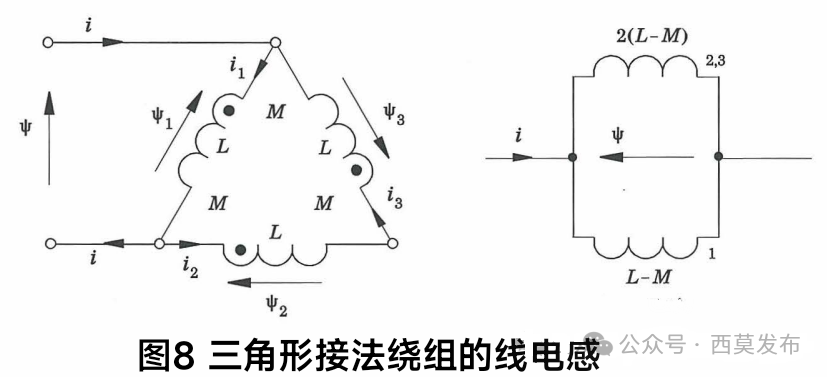
由图8可知,三角形接法时绕组的线电感:
Lʟʟ=(2/3)(L-M) (23)
将⑻式和⑼式中相应的自感和互感代入(23)式,并整理后(推导过程略)同样会得到一个与转子位置有关的线电感表达式,随着转子位置角θ的不同,同样会有一个最大值Lmax和一个最小值Lmin,对于内嵌式永磁电机:
Lmax=(2/3)Lq
Lmin=(2/3)Ld(24)
对于电励磁凸极同步电机:
Lmax=(2/3)Ld
Lmin=(2/3)Lq(25)
以上(21)、(22)、(24)、(25)各式反映了凸极同步电机线电感与交直轴电感之间关系,式(21)和式(22)适用于Y型接法的绕组,式(24)和式(25)适用于三角形接法的绕组。由于线电感往往比较容易测得的,因此可以利用这一关系来实测电机的交直轴电感。
5、电励磁同步电机的瞬变电感和交超瞬变电感
在电励磁同步电机中,转子直轴上会布置有励磁绕组,交直轴上还都布置有阻尼绕组,这些绕组都会与定子绕组存在互感。由电机学知识可知,如果把励磁绕组和阻尼绕组都看作超导体绕组,那么这些超导绕组会产生阻止磁通穿越它的作用,这样在瞬态时定子交直轴绕组产生的磁通会被迫排挤到漏磁路中,磁导大幅减小,此时交直轴绕组所反映出的电感远小于稳态时的Ld、Lq,我们分别称之为直轴超瞬变Ld″和交轴超瞬变电感Lq″;若只有直轴励磁绕组为超导,阻尼绕组开路,则磁通可以穿越阻尼绕组却无法穿越励磁绕组,这样直轴电感会小于直轴稳态电感Ld但大于直轴超瞬变电感Ld″,我们称之为直轴瞬变电感记为Ld′,Ld″<Ld′<Ld;由于交轴上无励磁绕组,故不存在交轴瞬变电感问题。
三、电机绕组各种电感之间的关系及测试方法
以上介绍了交流电机电枢绕组的各种电感,小结一下:
对称转子的交流电机,无论是各绕组独立的电感还是“三相系统”下的主电感都是恒定值,与转子位置无关。在异步电机和隐极同步电机稳态分析时,常采用“三相系统”下的主电感(抗)参数,等效电路中的激磁电感(抗)和电枢反应电感(抗)都是指“三相系统”下的主电感(抗)参数。
非对称转子的交流电机,虽然有三相绕组独立的自感和互感,但这些电感参数不是一个恒定值,而是随转子位置的不同而变化的值,如式⑻、式⑼所示,由于在电机旋转时这些参数都是时变参数,极其繁杂,因此这些参数在稳态分析时并不常用,只是在系统动态仿真时偶有应用。在凸极电机稳态分析时,常采用双反应理论来进行分析,因此必须经过一系列的坐标变换,得到直轴电感Ld和交轴电感Lq,需要说明的是,交直轴电感也是“三相系统”下的电感参数。关于交直轴电感参数与各相绕组独立的自感和互感参数之间的关系见⒁、⒃、⒅式。
由于三相绕组是物理存在的实际绕组,它们的自感和互感虽然繁杂,但物理意义非常清晰,且都能够通过实测的方法直接得到这些参数。而交直轴绕组由于不是实实在在物理存在的绕组,而是为了简化分析在数学上虚构的绕组,因此直接测量交直轴电感比较困难。在工程实践中,常通过采用测试线电感的方法来间接地得到交直轴电感。具体测试方法可以用RLC测试仪直接测量三相绕组的线电感,测量时缓慢转动转子,测得线电感的最大值和最小值,然后根据(21)、(22)、(24)、(25)各式中适应的电机类别计算出相应电机的交直轴电感。当然也可以采用在两相绕组的出线端直接加适当的(低压)工频交流电压,测量电流,然后用欧姆定律计算出线间电抗,得到线电感。
除了上述方法间接测量交直轴电感外,还可采用如图9所示的接法间接测量交直轴电感。
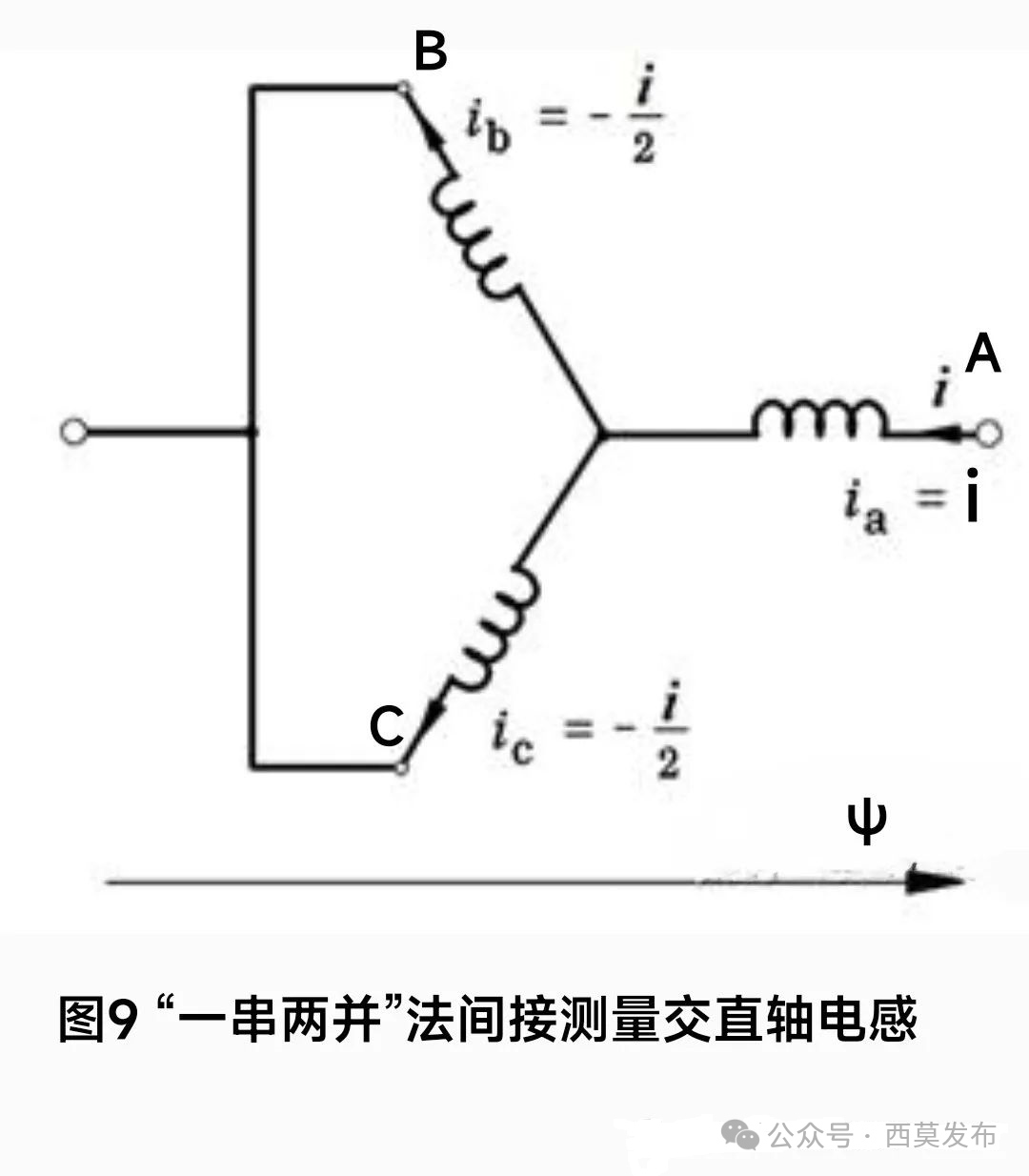
这种接法也称为“一串两并”接法,即将B、C两相绕组并联在一起,形成一个新的端点,用RLC测试仪或其他装置测量该端点和A相绕组端点之间的电感。通过缓慢转动转子,同样也可以测得一个电感的最大值Lmax和一个最小值Lmin,Lmax和Lmin与Ld和Lq的关系如下(推导过程略):
对于内嵌式的永磁同步电机
Lmax=(3/2)Lq
Lmin=(3/2)Ld (26)
对于电励磁的凸极同步电机
Lmax=(3/2)Ld
Lmin=(3/2)Lq (27)
需要特别说明的是,上述测试方法,无论是用RLC测试仪还是加工频交流电压进行测试,本质上都是在绕组上施加了交流测试电源。对于永磁电机而言,这种测试方法测得的线电感是磁路工作点附近的切线电感;对于电励磁同步电机,这种测试方法测得的线电感是不饱和值,这是因为测量时施加的电压较低,磁路处于不饱和状态,而且这种方法测得的线电感是超瞬变状态下的线电感,因为对于交流电而言,转子上的阻尼绕组会起到阻碍主磁通穿越阻尼绕组的作用,只有阻尼绕组开路时,这种方法测得的才是稳态交直轴电感,而对于一台制造完成的电机,阻尼绕组不可能开路,因此对于有阻尼绕组的电励磁同步电机不适合用这种测试方法来测试稳态交直轴电感,只能采取其它方法。关于交直轴电感的其它测试方法可参见GB/T1029,在此不赘述。
四、各种电感的用途
以上介绍了交流绕组的各种电感,它们各自都有什么用途呢?
首先,从宏观上讲,电机绕组的电感是电机的固有参数,决定着电机的各项主要性能,只有知道了这些电感,才能列写出各种平衡方程式、得到电机的等效电路、分析电机的各种性能。
其次,电机控制需要知道这些电感参数,以便搭建准确的控制模型,进行精确控制。通常控制系统会根据电机的各种参数建立一个控制所需的数学模型,根据数学模型计算出所要控制量的给定值,通过与反馈量的比较得到差值,然后再通过PID或其它控制方法进行控制。这些电感参数可以由制造商在出厂试验中测得,也可以通过控制软件中自带的参数自学习识别功能得到,为了更精确地实施控制,提高动态控制精度,对于非线性电感参数,有时需要采用状态扫描的办法事先对参数进行标定,得到不同运行状态下的参数。
第三,在电机制造过程中,可以通过测量绕组的三相电感,通过其平衡性来判断或诊断绕组的接线是否存在错误,是否存在电路方面的故障等。
第四,前面的介绍中讲到电感参数有视在电感(割线电感)和增量电感(切线电感)之分,许多同学不清楚什么时候应该用视在电感,什么时候应该用增量电感。这要视具体情况,一般在做稳态分析时,通常用视在电感,而在做瞬态分析时,往往要用增量电感,特别是永磁电机的控制模型中,电感后面带di时会用到增量电感。例如:内嵌式永磁电机的磁链为:
ψd=ψf+Ld*id
ψq=Lq*iq
以上两式中的Ld和Lq就应该用视在电感,而永磁电机的电压方程:
ud=id*R₁+Ld*p(id)-ωLq*iq
uq=iq*R₁+Lq*p(iq)+ω(ψf+Ld*id)
式中:p为微分算子,p=d/dt。以上两式中p后面的Ld和Lq就应该用增量电感。
本文为西莫首席技术专家李保来老师(西莫ID:标准答案)原创文章,本期期刊西莫视角栏目收录,并由西莫电子期刊主编hahafu整理发布以飨读者。
AIP艾普专注全球测试,以上信息来源网络,如有侵权请联系作者更改。
 鲁公网安备37021302000917号
鲁公网安备37021302000917号